Dune erosion
Definition of Dune erosion:
Sand loss from a dune under wave attack, mainly by notching, avalanching and slumping processes.
This is the common definition for Dune erosion, other definitions can be discussed in the article
|
This article deals with dune erosion by storms and provides some simple rules from which retreat of the dune front can be estimated.
Contents
Introduction
Coastal dunes have developed naturally along many shorelines worldwide during the last millennia when sea-level rise slowed down. Wave action and onshore winds are the main agents for coastal dune development and sufficient sand supply to the coast is a primary condition [1]. The coastal dune belt in many cases protects low-lying hinterland from flooding by the sea. Dune erosion therefore can be a serious threat.
A coastal dune can suffer large losses when attacked by storm waves. The front dune can be taken away over several tens of meters, leaving a steep dune scarp, see Fig. 1. For the Dutch coast it has been estimated that the dune foot can recede as much as 80-100 m under exceptional circumstances (extreme storms of very long duration, which may occur with a yearly probability of 1/100,000). The actual dune loss depends on local conditions such as beach width, beach height and dune height.
If at least part of the dune belt survives the storm, it can recover by natural processes – the same processes that created the original dune. This will happen only if the conditions under which the dune belt was formed – sand supply, wave and wind climate – have not significantly changed.
As an example, Fig. 2 shows a model result of the relationship between dune retreat [math]RD[/math] (expressed as the distance between the initial dune foot location and the dune foot location after the storm surge) and exceedance frequency (the probability that in a particular year a storm occurs that produces greater erosion) for a location along the Dutch coast. According to this figure there is a 1/100,000 probability per year that dune erosion will exceed 85 m.
To establish such a plot, a proper insight is needed in the possibly occurring extreme storm conditions in the (very) small probability range. However, such insight is subject to great uncertainty, as reliable measurements of extreme water levels and wave conditions are available only over relatively short periods of the order of 100 years. With such a restricted data set, it is hard to make estimates of storm conditions with a yearly exceedance probability less than about 1/1000.
Impact of dune erosion
Buildings on the front dune situated close to the dune foot are at risk under severe storms, see Fig. 3. A sound estimate of potential dune erosion is required when issuing building permits. In cases where the hinterland is situated below sea level, the dune belt serves as sea defence. Breach of the dune belt may have catastrophic consequences. Dune and beach monitoring and dune management are of crucial importance. In some cases, where the dune belt consists of a single dune row, dune reinforcement or shore nourishment may be needed. To ensure safety, several methods have been developed for estimating dune loss during exceptional storm conditions.
Brief explanation of dune erosion processes
The initial cross-shore beach profile, which might be considered to be in a more or less dynamic equilibrium condition with normally occurring hydrodynamic conditions, will be reshaped during a severe storm surge. The much higher water levels and much higher wave heights and peak periods call for a quite different shape of an equilibrium profile than the shape of the initial profile. Offshore directed sediment transports will occur, especially with sand eroded from the dunes.
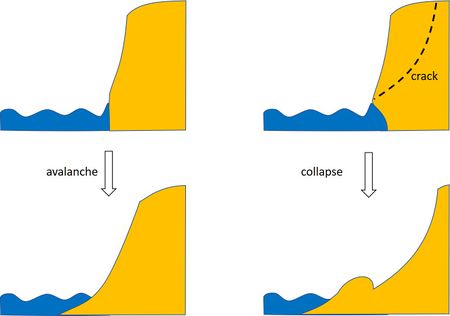
Wave attack at the dune foot steepens the dune profile which may collapse by avalanching (Fig.4). Wave attack may also create a notch at the dune foot leading to mass failure: collapse of a dune slab, initiated by tensile cracking at the top surface of the dune followed by shear failure along an internal failure plane or overturning due to the weight of the overhang [2], see Fig. 5.
The sand deposited at the dune foot is removed by the seaward undercurrent ('undertow') under the breaking waves and deposited on the shoreface. The slope of the cross-shore profile gradually decreases, and consequently the rate of dune erosion will decrease with time during the storm surge. It is, however, not expected that a new equilibrium profile will develop because of the limited storm surge duration. The shape of the cross-shore profile after the storm surge, which is a transient state between the initial profile and the storm equilibrium profile, is often called 'storm erosion profile'.
Quantification of dune erosion
Although 3D effects are undoubtedly important in the dune erosion process, often a 2D approach is adopted. In this case the dune erosion process is considered as a typically offshore directed cross-shore sediment transport problem. Sand from the dunes is transported to deeper water and settles there.
A first approach consists of assuming a closed sediment balance in cross-shore direction. The same volume of sand which is eroded from the dunes and the very upper part of a cross-shore profile is accumulated lower in the cross-shore profile. [Because of differences in porosity of the eroded dune material (often loosely packed) and the settled material (often a bit more densely packed), the sediment balance is not always strictly closed.]
During severe storm surges, with a great water level increase (a water level increase of a few metres is possible along some coasts) huge volumes of sand from the dunes are transported in offshore direction. And because dune erosion is a rather short lasting process, some computation methods take only offshore directed transports into account.
Erosion profile method
A quick first order estimate of storm dune erosion can be obtained by assuming that the storm erosion profile is close to the storm equilibrium profile. This assumption is unrealistic for storms of short duration and strongly overestimates storm dune erosion in this case. However, for storms of very long duration, which produce great dune losses with low exceedance probability, the assumption of a post-storm equilibrium profile is not unreasonable. The method is still used in the Netherlands, besides other more advanced methods, to provide an upper bound of possible storm dune erosion. It is based on empirical post-storm equilibrium profiles established by laboratory experiments and validated by field data of the Dutch coast [3]. The post-storm equilibrium profile was established for different values of the significant wave height [math]H[/math], peak wave period [math]T[/math] and mean fall velocity of dune sand [math]w[/math]. Major assumption are:
- the storm duration is sufficient for establishment of a post-storm equilibrium profile [math]y(x)[/math];
- the post-storm equilibrium profile does not (strongly) depend on the initial coastal profile [math]y_0(x)[/math];
- eroded dune sediment is deposited within a zone delimited by a storm closure depth [math]y_{max}[/math];
- the eroded dune scarp has a slope 1:1 and the slope at the toe of the sand deposit is 1:12 (these are less crucial assumptions).
With these assumptions the eroded dune volume is given by the beach volume between [math]y(x)[/math] and [math]y_0(x)[/math], such that the total sand volume landward of the closure depth [math]y_{max}[/math] is preserved. The procedure is explained in Fig. 6, where the parameterized functions for the post-storm equilibrium profile [math]y(x)[/math] and the storm closure depth [math]y_{max}[/math] are also indicated.
The slope of the post-storm profile decreases (i.e. increasing dune erosion) as the wave period [math]T[/math] increases and the fall velocity decreases. A serious drawback of this straightforward method is that hardly any physics is involved. The development with time of the storm profile is unknown. Effects of varying water levels and varying wave characteristics during the storm surge cannot be accounted for.
Analytic dune erosion model
A simple analytic model was developed by Larson et al. (2004[4], 2016[5]) for estimating the time evolution of dune erosion. This model is based on the assumption that the eroded dune volume [math]\Delta V[/math] in a time interval [math]\Delta t[/math] is proportional to the force [math]F[/math] exerted by swash waves hitting the dune foot. By expressing the force [math]F[/math] as a function of the dune foot height [math]z_D[/math], the wave run-up [math]R[/math] and the wave period [math]T[/math], the following equation was obtained for the loss rate [math]dV/dt[/math] of dune volume (see the appendix and Fig. B1):
[math]\Large\frac{dV}{dt}\normalsize=-4C_s\Large\frac{(R-z_D)^2}{T}\normalsize , \qquad (1)[/math]
where the site-dependent constant [math]C_s[/math] has to be determined empirically. According to this equation, the rate of dune erosion is an increasing function of the wave height, the wave period and the beach slope (see appendix). This is consistent with the dune erosion estimate following from the storm profile of Fig. 6. Equation (1) also shows that dune erosion strongly depends on the height [math]z_D[/math] of the dune foot (i.e. on the beach steepness). This is consistent with observations at Narrabeen-Collaroy Beach (East Australia, near Sidney), which showed that alongshore variability in dune erosion was strongly correlated with alongshore variability in [math]z_D[/math][6]. Assuming that the beach slope [math]\beta[/math] remains constant during dune erosion (i.e., dune retreat [math]\Delta x[/math] equal to [math]\Delta z_D / \tan \beta[/math]), Larson et al. (2004[4]) found reasonable agreement with observed dune erosion rates when using the parameterization [math]C_s=1.34 \, 10^{-3} \exp(-3.19 \, 10^{-4} H/d_{50})[/math], where [math]d_{50}[/math] is the median sediment grainsize and [math]H[/math] the root-mean-square wave height during the storm.
DUROSTA
Based on theoretical work and laboratory experiments, Steetzel (1993) [7] has developed the 2-dimensional DUROSTA computation model, in which actual sediment transports are calculated based on wave-integrated velocity and sand concentration profiles. Although in the mathematical description of the cross-shore sediment transport the intra-wave component is neglected, the results of the model compared well with large scale model tests in the Delta Flume of Delft Hydraulics. During storm surge conditions, breaking waves in the surf zone cause a strong return flow in the lower part of the water column and high sediment concentrations throughout the water column. The cross-shore profile is updated at each time step, based on gradients in the computed sediment fluxes. The DUROSTA model therefore provides estimates of the time evolution of the dune and beach profiles during a storm surge.
XBeach
XBeach [8] is an open-source process-based numerical model that was originally developed to simulate hydrodynamic and morphodynamic processes and impacts on sandy coasts with a domain size of kilometers and on the time scale of storms. Since then, the model has been applied to other types of coasts and purposes. The model includes the hydrodynamic processes of short wave transformation (refraction, shoaling and breaking), long wave (infragravity wave) transformation (generation, propagation and dissipation), wave-induced setup and unsteady currents, as well as overwash and inundation. The morphodynamic processes include bed load and suspended sediment transport, bed update and breaching. Effects of vegetation and hard structures have been included. The model has been validated with a series of analytical, laboratory and field test cases using a standard set of parameter settings. The avalanching of sandy material from the dune face to the foreshore during storm conditions is taken into account when updating the bed levels. This is modeled through introduction of a critical bed slope (default critical slope of 1 for dry zones and 0.3 for wet zones). When the critical slope is exceeded, material is exchanged between adjacent cells to the amount needed to bring the slope back to the critical slope.
Comparison with observed dune erosion events at the Dutch coast show that XBeach estimates the magnitude and pattern of alongshore variations in erosion volume reasonably well. The 2014-version of XBeach overpredicted the erosion volume in the region where a dune scarp developed and underestimated the erosion volume where the whole dune face collapsed in a series of slumps [9]. XBeach simulations further illustrated that the observed alongshore variation in dune erosion was steered primarily by the pre-storm dune topography i.e., the presence of embryonic dune fields and the steepness of the dune face. The importance of alongshore variability in intertidal beach topography was found to be secondary, but not negligible during the initial stage of the storm, when the surge level was still low. An application of the 2019 version of XBeach to a breach experiment at a large-scale sand dune in Germany showed that the post-storm beach profile was well simulated, but dune erosion was overestimated with respect to temporal profile evolution. It was concluded that the XBeach model is capable of accurately predicting the evolution of storm-induced erosion during a sufficiently long and overwash/inundation-dominant surge event when current high-resolution input data is available[10].
Post-storm dune recovery
After being eroded under storm conditions, the dune front can recover naturally without human intervention. This has been observed for many sandy coasts with either a gently sloping or a steep sloping shoreface [11][12][13]. After-storm recovery starts with the development of embryo dunes on the backshore and is stimulated by vegetation growth on these embryo dunes[14]. An example of natural dune recovery is shown in Fig. 7 for a retreating coast (Walcheren, the Netherlands). The extreme storm surge of 1953 caused a 30m retreat of the dune foot. Afterwards the dune foot advanced slightly over a period of several years, until it reached about 15 years later the position corresponding to the retreating trend prior to the storm surge. The ongoing coastal retreat was finally halted in 1990, when the Dutch government decided to stop coastal retreat along the entire coastline by coastal sand nourishments. Recovery of the shoreline precedes recovery of the dune foot and is much faster. Fig. 8 shows after-storm recovery of the shoreline position at Narrabeen-Collaroy Beach in East Australia, near Sidney. The recovery period after each storm-induced shoreline retreat is only a few months at this location. Shoreline recovery at this location is significantly correlated with onshore migration of nearshore sand bars[13][15].
 Fig. 7. Variation of the dune foot position in a beach transect of the island Walcheren (Netherlands) over the period 1900-2010 (solid white line, based on annual surveys of Rijkswaterstaat [16]). The trend is indicated by the dashed line, showing ongoing retreat of the dune foot from 1900-1990. The large dune erosion by the exceptional 1953 storm surge has no influence on the long-term trend of dune foot retreat. Stabilization after 1990 is due to implementation of the current 'hold-the-line' coastal policy by sand nourishments. |
 Figure 8. Variation of the shoreline position in a transect of Narrabeen-Collaroy Beach (East Australia, near Sidney) over the period October 2004-May 2005. Strong shoreline retreat occurs during the storm periods indicated in light blue. After-storm recovery occurs during the periods in between. Figure redrafted after [13]. |
Impact of sea-level rise on dune erosion
The XBeach model predicts a linear relationship between dune erosion volume and sea level rise [17]. This is primarily due to the higher water level in front of the dune and not to changes in the significant short-wave or infragravity wave height. Changes in the offshore angle of wave incidence also affect the dune erosion volume. A 30° shift from shore-normal influences the dune erosion volume to the same extent as a 0.4 m sea-level rise. This increase in dune erosion volume is related to strong alongshore currents, generated as a result of the obliquity of the waves, that enhance stirring and hence offshore transport.
The model simulations further show that the effectiveness of coastal sand nourishment to mitigate the impact of sea-level rise, strongly depends on the location in the profile where this sand is added. However, the ratio of the reduction in dune erosion volume to the total added volume remains low (<0.3) for all mitigation options. This suggests that directly increasing the volume of sand in the dunes may be more efficient from a morphological perspective.
Appendix: Analytical dune erosion model
The analytic model of Larson et al. (2004[4]) is based on the following assumptions and simplifications:
- The eroded dune volume [math]\Delta V[/math] in a time interval [math]\Delta t[/math] is proportional to the force [math]F[/math] exerted by swash waves hitting the dune foot, [math]\Delta V \propto F \Delta t .[/math]
- The force [math]F \Delta t [/math] is proportional to the number of swash bores [math]n[/math] hitting the dune foot ([math]n=\Delta t/T[/math]) and the force exerted by each individual swash bore, [math]f=m \Large\frac{du}{dt}\normalsize \propto \Large\frac{mu}{T}\normalsize [/math], where [math]T[/math] is the wave period, [math]m[/math] the mass of the swash bore per unit dune width and [math]u[/math] the velocity of the swash bore when hitting the dune foot.
- The bore height [math]h[/math] is related to the bore velocity by [math]u \propto \sqrt{gh}[/math], where [math]g[/math] is the gravitational acceleration. The bore mass is thus proportional to [math]m \propto huT \propto u^3 T[/math], yielding [math]F = n \,f / \Delta t \propto u^4 /T[/math].
- The bore velocity at the dune foot can be related to the swash runup [math]R[/math]. A ballistic swash excursion model (neglecting friction) gives an estimate for this relation, [math]R=z_D+gu^2/2[/math], where [math]z_D[/math] is the height of the dune foot compared to the beach level where waves collapse on the beach. Using this relation, the force [math] F [/math] can be expressed as a function of the wave runup [math] R [/math], [math]F \propto (R – z_D)^2 / T[/math].
- Substitution with [math]\Delta V / \Delta t \approx dV/dt [/math] gives Eq. (1), where [math]C_s[/math] is a proportionality constant, depending on characteristics of the site, such as sediment grainsize, wave incidence angle, shoreface profile, etc. The coefficient [math]C_s[/math] should be determined empirically; usual values are found in the range [math]10^{-3}\; - \; 2.5\;10^{-3}[/math].
- The wave run-up [math]R[/math] depends on the beach slope [math]\beta[/math], the offshore wave height [math]H[/math] and wave period [math]T[/math]; an approximate empirical expression is [math]R \sim \tan \beta \sqrt{HL} [/math], where [math]L \approx g T^2/2 \pi[/math] is the offshore wavelength (see also Swash zone dynamics for more details).
Substitution in Eq. (1) gives [math]\Large\frac{dV}{dt}\normalsize = -4C_s \tan \beta (\sqrt{\Large\frac{gH}{2 \pi}\normalsize } - \Large\frac{l}{T}\normalsize) [/math], where [math]l[/math] is the beach width, which increases as the dune foot retreats.
This expression shows that the rate of dune erosion increases as the wave height [math]H[/math] increases, the wave period [math]T[/math] increases and the beach slope [math]\beta[/math] increases.
The dune foot height [math]z_D[/math] (relative to the beach level of wave collapse [math]z_C[/math]) and the beach slope [math]\beta[/math] are time dependent. In order to solve Eq. (1) a prescription must be given how the eroded dune material is distributed over the beach – i.e. a model for the dependence of [math]z_D[/math] and [math]\beta[/math] on [math]dV/dt[/math]. Based on experiments in large wave flumes, Larson et al. (2004[4])assumed that the beach slope [math]\beta[/math] remains constant during dune erosion. The dune retreat [math]\Delta x[/math] was therefore set equal to [math]\Delta z_D / \tan \beta[/math], assuming that the major part of the dune volume loss is removed to the lower beach (below the level of wave collapse). Considering a dune height [math]D[/math] above the level of wave collapse [math]z_C[/math], the loss of dune volume is given by [math]\Delta V=-(D-z_D) \Delta x = -(D- z_D) \Delta z_D / \tan \beta[/math]. Combining this result with Eq. (1) yields a differential equation for the dune foot height [math]z_D[/math]:
[math]\Large\frac{d}{dt}\normalsize z_D = \Large\frac{1}{\tau} \frac{(R-z_D)^2}{D-z_D}\normalsize , [/math] where [math]\tau=T/(4 C_s \tan \beta)[/math].
If it is further assumed that the level of wave collapse [math]z_C[/math] does not change during the storm, then the wave run-up [math]R[/math] remains constant too (the slope [math]\beta[/math] was assumed constant). The differential equation can then be solved, with solution
[math]t = \tau (D-R)\Large(\frac{1}{R-z_D(0)} - \frac{1}{R-z_D(t)})\normalsize +\tau \ln\Large\frac{r-z_D(0)}{r-z_D(t)}\normalsize [/math], from which [math]z_D(t)[/math] and [math]V(t)[/math] can be derived.
Related articles
- Dune stabilisation
- Light revetments built-in into artificial dunes
- Natural causes of coastal erosion
- Shoreface profile
- Bruun rule
- Risk and coastal zone policy: example from the Netherlands
- Swash zone dynamics
References
- ↑ Anthony, E.J., Mrani-Alaoui. M. and Héquette, A. 2010. Shoreface sand supply and mid- to late Holocene aeolian dune formation on the storm-dominated macrotidal coast of the southern North Sea. Marine Geology 276: 100–104
- ↑ Erikson, Li, H., Larson, M. and Hanson, H. 2007. Laboratory investigation of beach scarp and dune recession due to notching and subsequent failure. Marine Geology 245 (2007) 1–19.
- ↑ van Gent, M.R.A., van Thiel de Vries, J.S.M., Coeveld, E.M., de Vroeg, J.H. and van de Graaff, J. 2008. Large-scale dune erosion tests to study the influence of wave periods Coastal Engineering 55: 1041–1051
- ↑ 4.0 4.1 4.2 4.3 Larson, M., Erikson, L. and Hanson, H. 2004. An analytical model to predict dune erosion due to wave impact. Coastal Engineering 51: 675– 696
- ↑ Larson, M., Palalane, J., Fredriksson, F. and Hanson, H. 2016. Simulating cross-shore material exchange at decadal scale. Theory and model component validation. Coastal Engineering 116: 57–66
- ↑ Splinter, K.D., Kearney, E.T. and Turner, I.L. 2018. Drivers of alongshore variable dune erosion during a storm event: Observations and modelling. Coastal Engineering 131: 31–41
- ↑ Steetzel, H.J. 1993. Cross-shore transport during storm surges. Thesis Tech. Univ. Delft, Delft Hydraulics Communications 476.
- ↑ https://xbeach.readthedocs.io/en/latest/user_manual.html
- ↑ De Winter, R.C,. Gongriep, F. and Ruessink, B.G. 2014. Observations and modeling of alongshore variability in dune erosion at Egmond aan Zee, the Netherlands. Coastal Engineering 99: 167-175.
- ↑ Schweiger, C., Kaehler, C., Koldrack, N. and Schuettrumpf, H. 2020. Spatial and temporal evaluation of storm-induced erosion modelling based on a two-dimensional field case including an artificial unvegetated research dune. Coastal Engineering 161, 103752
- ↑ Vousdoukas, M.I., Pedro, L., Almeida, M. and Ferreira, O. 2012. Beach erosion and recovery during consecutive storms at a steep-sloping, meso-tidal beach. Earth Surf. Process. Landf. 37: 583–593
- ↑ Scott. T., Masselink, G., O'Hare, T., Saulter, A., Poate, T,. Russell. P., Davidson, M. and Conley, D. 2016. The extreme 2013/2014 winter storms: Beach recovery along the southwest coast of England. Marine Geology 382: 224–241
- ↑ 13.0 13.1 13.2 Phillips, M.S., Harley, M.D., Turner, I.L., Splinter, K.D. and Cox , R.J. 2017. Shoreline recovery on wave-dominated sandy coastlines: the role of sandbar morphodynamics and nearshore wave parameters. Marine Geology 385: 146–159
- ↑ Suanez, S., Cariolet, J-M., Cancouët, R., Ardhuin, F. and Delacourt, C. 2012. Dune recovery after storm erosion on a high-energy beach: Vougot Beach, Brittany (France). Geomorphology 139-140: 16–33
- ↑ Brooks, S.M., Spencer, T. and Christie, E.K. 2017. Storm impacts and shoreline recovery: Mechanisms and controls in the southern North Sea. Geomorphology 283: 48–60
- ↑ Jeuken, C., Ruessink, G. and Marchand, M. 2001. Ruimtelijke en temporele aspecten van de duinvoetdynamiek. Report WL/Delft Hydraulics Z2838 (in Dutch)
- ↑ De Winter, R,C. and Ruessink, B.G. 2017. Sensitivity analysis of climate change impacts on dune erosion: case study for the Dutch Holland coast. Climatic Change (2017) 141:685–701 DOI 10.1007/s10584-017-1922-3
Please note that others may also have edited the contents of this article.
|